e is one of the most famous numbers of mathematics with an approximate value of 2.71828 and contributes in an extraordinary manner to describe, quantify, and resolve in particular problems in medicine, physics, chemistry, or pharmacy where growth, decay, absorption, metabolism, and elimination play important roles. There are different concepts of establishing a method to represent steady growth which all are finally based on e. As Crilly describes in his book „50 mathematical ideas you need to know“ (1) one of these concepts was developed by Jacob Bernoulli. Interestingly however, when he set to work in 1683 he wanted to resolve the financial problem of compound interest. His idea was to divide a period of time, for example one year, into equal parts such as half years, quarters, months, and days as well as the interests whereby the principal was increased by the interest accrued at the end of each part passed. The principal in this case may be 1 currency unit, for example 1 $, which should yield in the calculation according to 100% interest another $ at the end of the year. The following table as shown by Crilly gives an overview:
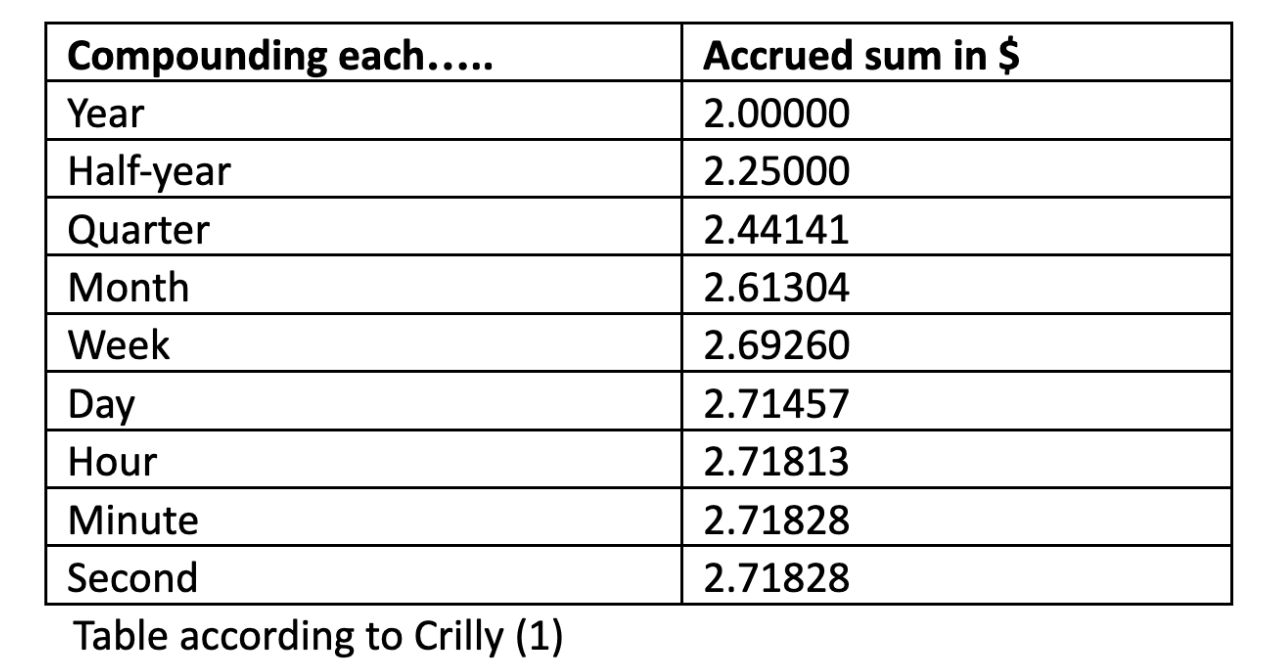
It is easily recognized that the Bernoulli concept of splitting the base period into infinitely small parts of time leads finally to a marginal limit which is e. The number 2.71814593 which comes close to e was already described in the logarithm table which the suisse mathematician Buergi had computed in the years 1603-1610 (2). It was however Bernoulli who concluded that the steady growth cannot surpass a limit which is set through the number 2.71828.
Crilly points then to another method to compute e. In 1748 Euler who was indeed the first to introduce the name „e“ computes this number as the marginal limit of the following series expansion containing up to the infinite growing faculties in the denominator (3), see Formula a) :
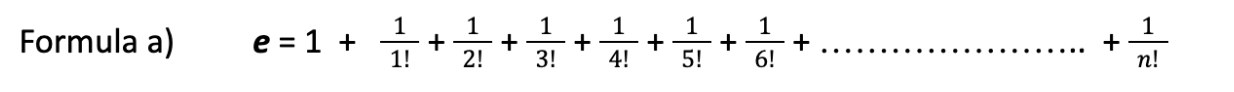
Thus, Euler computed the value of e with 2.71828182845904523536028 (3).

Crilly points then to another method to compute e. In 1748 Euler who was indeed the first to introduce the name „e“ computes this number as the marginal limit of the following series expansion containing up to the infinite growing faculties in the denominator (3), see Formula a) :
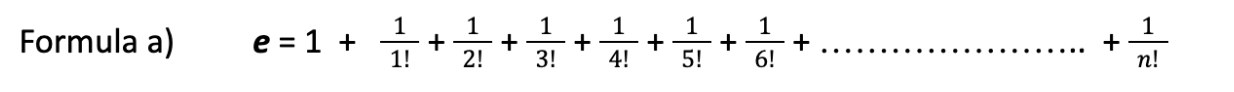
Thus, Euler computed the value of e with 2.71828182845904523536028 (3).

With decreasing h towards 0 the marginal limit for e may be computed to 2.7182818….
The Bernoulli concept described above, however, opens the door also to another approach to assess the value of e.
If the base period of a year is not split and the interest rate which accrues to the principal is 100% we compute the sum of principal plus interest for the year in $: 1 + 1 = 2 .
If we split the year into n = 2, 3, 4 or more parts and add the interest of each part of time at the end to the principal we get the following computations for
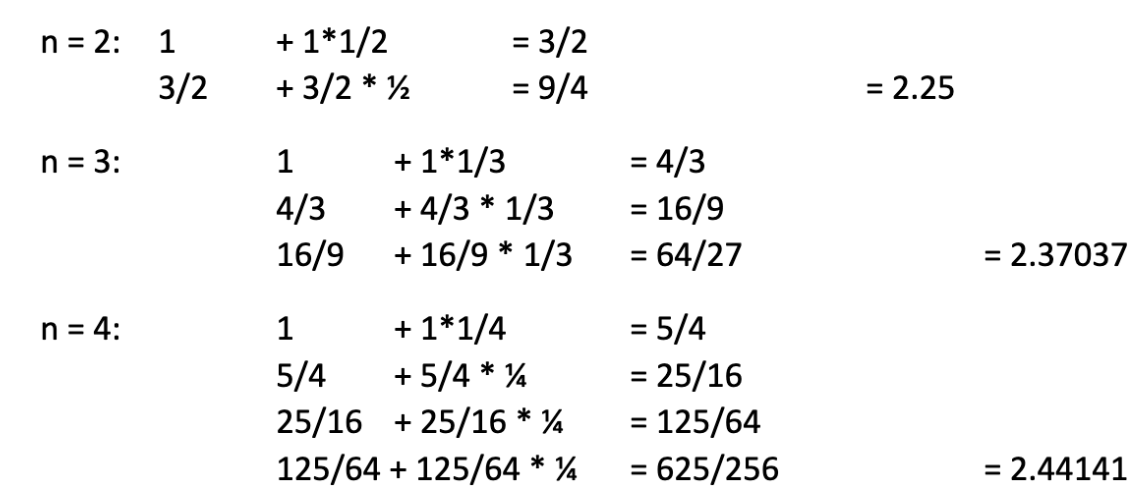
As shown the procedure becomes quickly tedious; when, however modifying the „Crilly“-table presented above and introducing potencies in numerator and denominator to represent the values computed a possible order becomes visible:
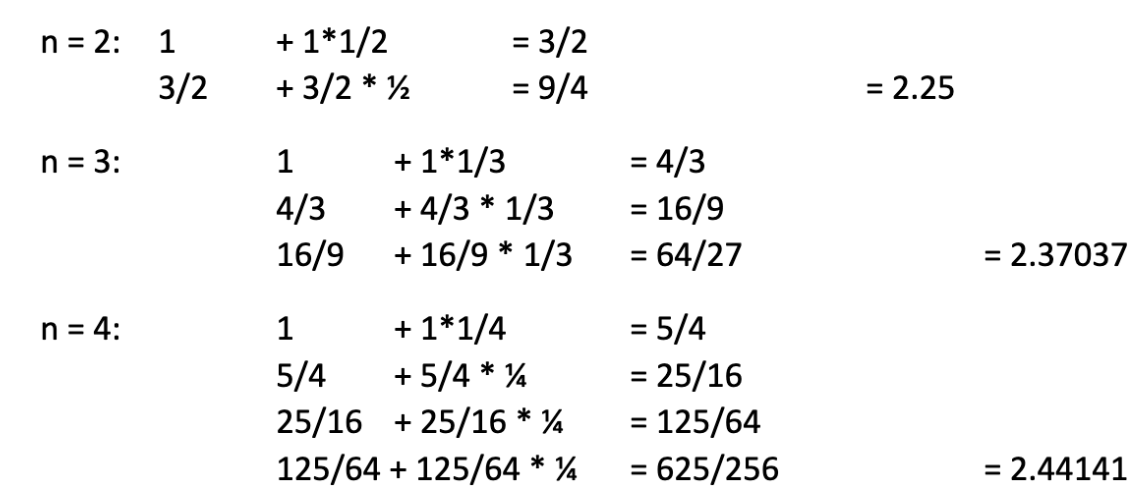
As shown the procedure becomes quickly tedious; when, however modifying the „Crilly“-table presented above and introducing potencies in numerator and denominator to represent the values computed a possible order becomes visible:
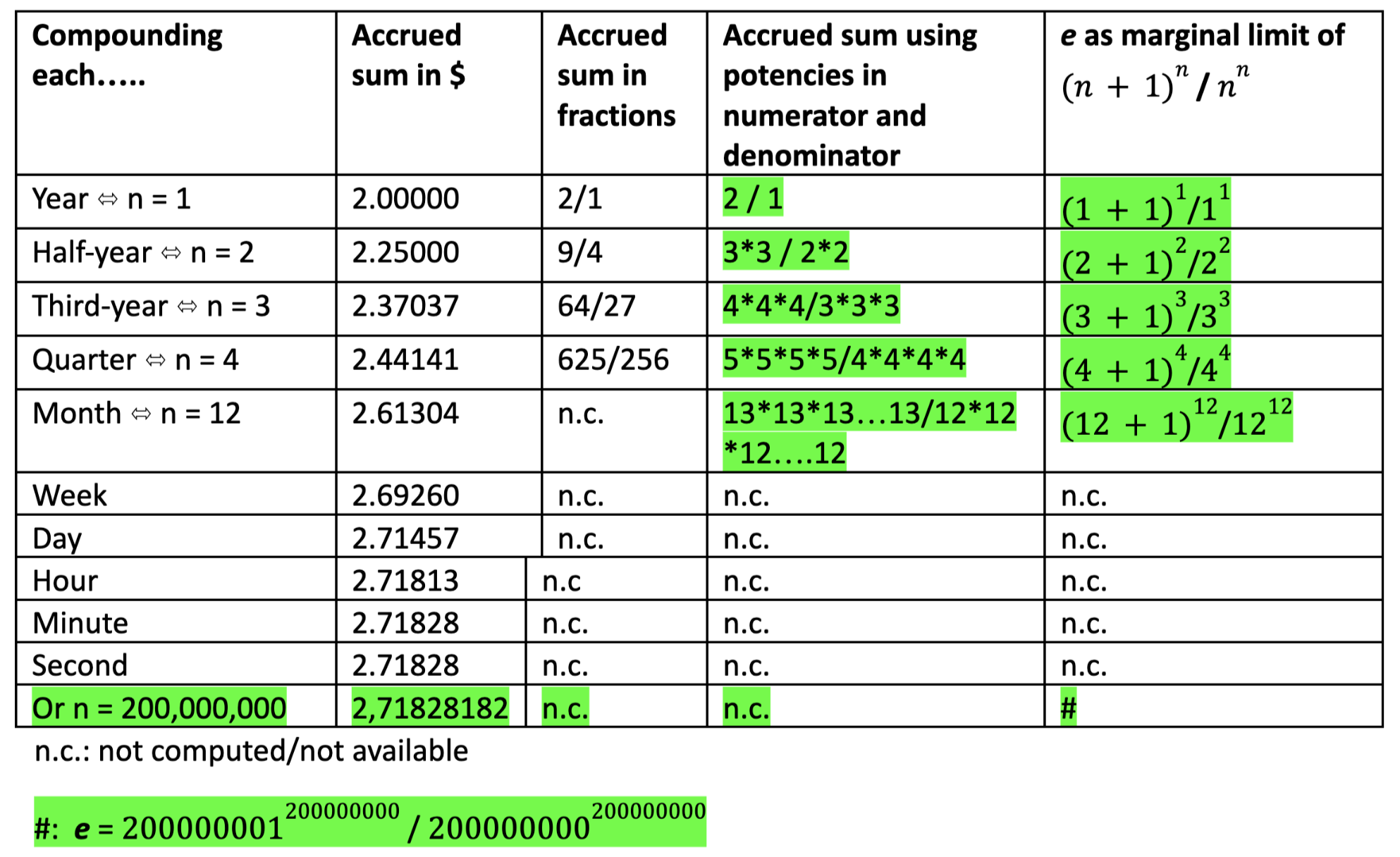
The conclusion is: Based on the transformation proposed the following formula c) may be induced:
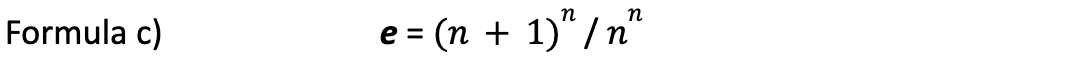
With n increasing to the infinite e may be computed with as many decimal places as wanted. Using the webservice wolframalpha.com (5) it can be shown that e can be computed in consistency with Euler’s value of 2.71828182 with n >= 200,000,000 .
The simplicity of Formula c) does not stand back behind that one of Formula a) or b).
Comments revealing that the assessment of e according to Formula c) has been described anywhere in the e-literature are highly appreciated.
Formula b) and its marginal limit for infinitely big n can also be expressed in the following way:
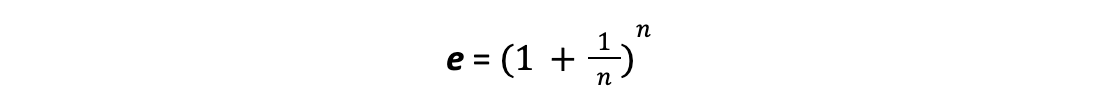
Therefore the following equation should apply based on the assumption that Formulas b) and c) are equivalent:
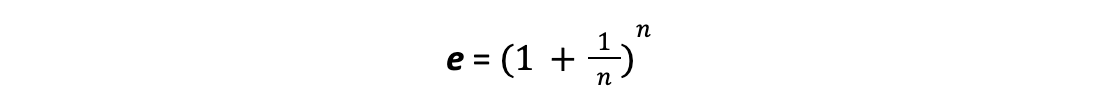
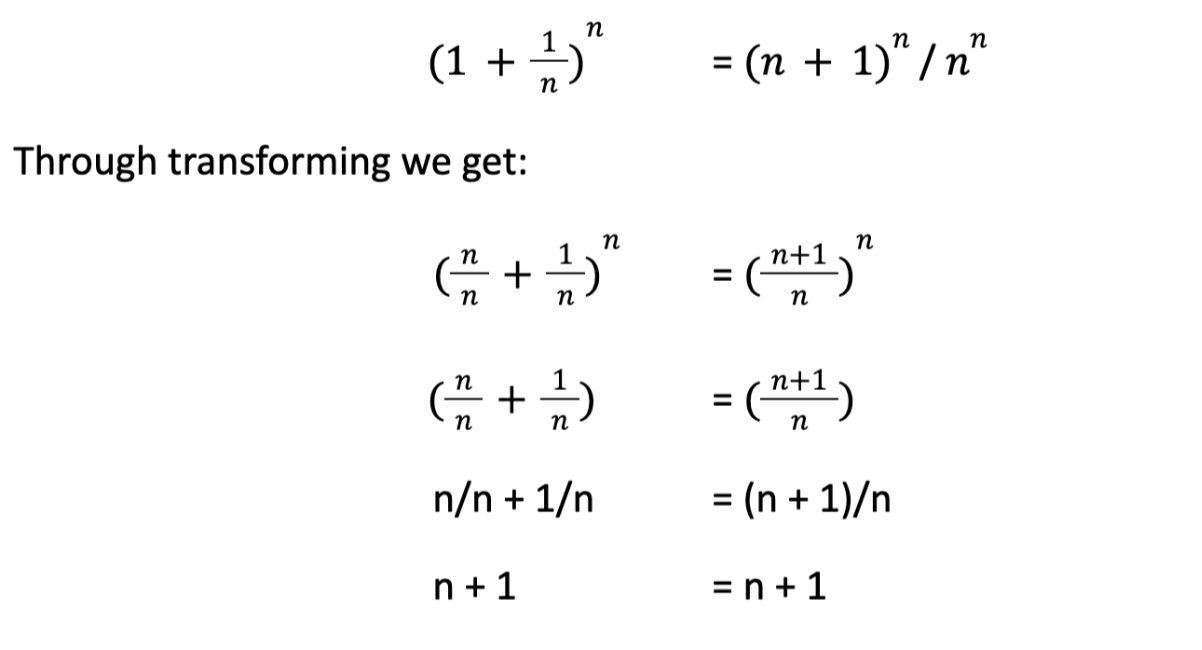
Wolfgang U. Scholz
Natural Scientist and Founder of SCHOLZ Databank
Comments and questions may be sent to
Natural Scientist and Founder of SCHOLZ Databank
Comments and questions may be sent to
Literature:
1) Crilly, Tony: 50 mathematical ideas you really need to know; Quercus Publishing Plc, London, 2007; p. 24-26
2) Schönhacker, Stefan: Die Zahl e; Diplomarbeit Universität Wien, 2007 (The number e, diploma thesis, University of Vienna, 2007)
3) Gonzalez-Velasco, Enrique A.: Journey through Mathematics; Springer LLC, New York, 2011; p. 139
4) Jordan, D.W. and P. Smith: Mathematical Techniques An Introduction for the Engineering, Physical and Mathematical Sciences, Oxford University Press, 1994; translated to german: Mathematik für die Praxis, Nikol Verlag, Hamburg, 2007, page 38
5) Wolframalpha.com